10296. Рекурсивная функция 1

Вычислите значение функции:

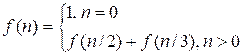
Вход. Одно натуральное число n (1 ≤ n ≤ 10¹⁸).

Выход. Выведите значение f(n).

Пример входа	Пример выхода
5	5

РЕШЕНИЕ

рекурсия - map

Анализ алгоритма

Для запоминания результатов значений функции f из-за ограничения n ≤ 10¹⁸ невозможно использовать линейный массив. Поэтому будем использовать структуру данных map.

Пример

Рассмотрим процесс вычисления функции для n = 5:

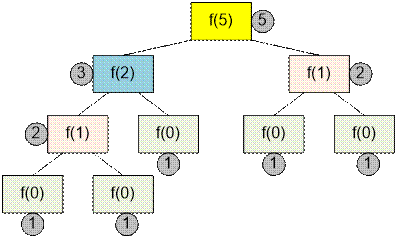
Реализация алгоритма

Объявим отображение m для хранения значений функции: m[n] = f(n). 

map<long long, long long> m;

Реализация функции f.

long long f(long long n)

{

if (n == 0) return 1;

if (m.count(n) > 0) return m[n];

return m[n] = f(n / 2) + f(n / 3);

}

Основная часть программы. Читаем входное значение n. Вычисляем и выводим значение функции f(n).

scanf("%lld", &n);

res = f(n);

printf("%lld\n", res);

Java реализация

import java.util.*;

public class Main

{

static Map<Long, Long> m = new HashMap<Long, Long>();

static long n;

public static long f(long n)

{

if (n == 0) return 1;

if (m.containsKey(n)) return m.get(n);

long res = f(n/2) + f(n/3);

m.put(n,res);

return res;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextLong();

System.out.println(f(n));

con.close();

}

}

Python реализация

Объявим словарь m для хранения значений функции: m[n] = f(n).

m = {}

Реализация функции f.

def f(n):

if n == 0:

return 1

if n in m:

return m[n]

m[n] = f(n // 2) + f(n // 3)

return m[n]

Основная часть программы. Читаем входное значение n. Вычисляем и выводим значение функции f(n).

n = int(input())

res = f(n)

print(res)